while (1): study();
Ch1. 신경망 복습 본문
대부분의 내용이 반복인 점을 감안하여 새롭게 알게 된 내용을 위주로 작성하겠습니다.
이전 1권에서 곱셈, 덧셈 등 노드에 대해서 어떻게 역전파를 계산하는지 알아봤습니다. 기본적으로 역전파는 '상류에서 흘러들어온 기울기를 편미분'하여 하류로 흘려보냅니다. 여기서는 이전에 제시하지 않았던 종류의 노드를 제시하고 있습니다. 바로 Repeat 노드입니다.

Repeat 노드의 순전파는 단순히 들어온 입력을 N번 복사하는 것입니다. 이는 np.repeat 함수로 쉽게 구현이 가능합니다. 반대로 역전파는 흘러들어오는 기울기에 대해서 모두 더해주는 과정입니다. 사실 Repeat 노드는 넘파이의 브로드캐스팅 기능으로 간단히 구현할 수 있기 때문에, 따로 모듈화할 필요는 없습니다.
이전의 기억을 잘 더듬어보면, 덧셈 노드 순전파 시 들어온 입력을 모두 더해주고, 역전파 시 기울기를 그대로 흘려보내줬습니다.

즉 Repeat 노드와 Sum 노드는 순전파와 역전파가 완전히 반대인 관계라는 것을 알 수 있습니다.
이번에는 MatMul 노드를 살펴보겠습니다.

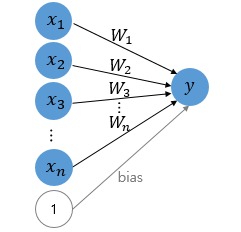
배치 단위로 입력이 들어왔을 때를 가정하면, 각각의 가중치의 형태는 위의 그림과 같습니다. 순전파 과정은 $xW = y$와 같이 계산되므로, $(N, D) * (D, H) = (N, H)$로 모양이 떨어집니다. 역전파 시에는 ${{\partial}L \over {\partial}y}$가 노드로 흘러들어옵니다. 손실에 대한 $x$의 편미분은 ${{\partial}L \over {\partial}x} = {{\partial}L \over {\partial}y} * {{\partial}y \over {\partial}x}$입니다. 따라서 ${{\partial}L \over {\partial} x}$ = ${{\partial}L \over {\partial}y} W^{T}$이며 $(N, D) = (N, H) * (H, D)$로 형태가 맞아 떨어지게 됩니다.
MatMul 노드는 다음과 같이 구현할 수 있습니다.
class MatMul:
def __init__(self, W):
self.params = [W]
self.grads = [np.zeros_like(W)]
self.x = None
def forward(self, x):
W = self.params[0]
out = np.dot(x, W)
self.x = x
return out
def backward(self, dout):
W = self.params[0]
dx = np.matmul(dout, W.T)
dW = np.matmul(self.x.T, dout)
self.grads[0][...] = dW
return dx이 때 self.grads[0][...]에서 생략기호는 메모리를 고정시키는 역할을 합니다. 예를 들어 그냥 self.grads[0] = dW라고 할 시 dW의 메모리 주소를 self.grads[0]이 공유하는 것이 됩니다. 그러나 self.grads[0][...] = dW를 사용할 시 dW와 self.grads[0]은 각각 다른 주소를 가지나, 같은 값을 가지게 됩니다. 결론적으로 얕은 복사와 깊은 복사의 차이입니다.
다음으로 Affine 계층은 다음과 같이 구현할 수 있습니다.
class Affine:
def __init__(self, W, b):
self.params = [W, b]
self.grads = [np.zeros_like(W), np.zeros_like(b)]
self.x = None
def forward(self, x):
W, b = self.params
out = np.matmul(x, W) + b
self.x = x
return out
def backward(self, dout):
W, b = self.params
dx = np.matmul(dout, W.T)
dW = np.matmul(self.x.T, dout)
db = np.sum(dout, axis=0)
self.grads[0][...] = dW
self.grads[1][...] = db
return dx
Matmul vs Dot
갑자기 문득 np.dot이랑 np.matmul의 차이점이 궁금해서 찾아보았습니다. 우선, np.dot은 모든 형태의 배열에 대해 연산이 가능하며 2차원 이하의 배열까지는 matmul과 결과가 동일합니다. 그러나 3차원 이상의 경우부터 차이가 납니다. 예를 들어 형태가 (a1, a2, a3, a4)인 배열과 (b1, b2, b3, b4)인 배열을 내적한다고 했을 때 np.dot은 a4와 b3가 같다면 연산을 수행하고, 결과로 (a1, a2, a3, b1, b2, b4) 형태의 배열을 반환합니다.
반면 np.matmul은 스칼라에 대해서 연산을 할 수 없는, 그야말로 선형대수학에 알맞는 연산입니다. 위와 같이 (a1, a2, a3, a4)인 배열과 (b1, b2, b3, b4)인 배열을 내적한다고 했을 때, np.matmul은 뒤의 두 축을 제외한 모든 차원에 대해서 형태가 같아야 합니다. 즉 a1과 b1, a2와 b2의 형태가 같아야 합니다. 또한 마지막 두 축에 대해선 a4와 b3의 크기가 같아야하고, 결과적으로 (a1, a2, a3, b4) 형태의 배열을 반환합니다.

정리하자면 다음과 같습니다.
| np.dot | np.matmul | ||||
| 연산 | (a1, a2, a3, a4) x (b1, b2, b3, b4) = (a1, a2, a3, b1, b2, b4) |
(a1, a2, a3, a4) x (b1, b2, b3, b4) = (a1, a2, a3, b4) |
|||
| 조건 | 1) a4 = b3 2) 모든 차원의 배열 |
1) a1 = b1, a2 = b2, a4 = b3 2) 스칼라와는 불가 |
|||
| 시간 | 느림 | 빠름 |
연산 시간에 대해서는 실험 결과를 가져왔습니다. 교재에서 제공하는 spiral 데이터셋에 대해서 2000에포크의 학습을 수행하기까지 걸린 시간을 비교해보겠습니다.

Matmul로 Affine 계층을 구현한 경우 5.22초가 걸렸습니다.

Dot으로 Affine 계층을 구현한 경우 8.49초가 걸렸습니다. 행렬 연산에 MatMul이 더 효과적이라는 사실을 알 수 있습니다. 실제로 넘파이 독스에서도 행렬의 계산에 MatMul연산을 사용할 것을 권하고 있습니다.
저는 위의 코드말고, 기존에 짜놓은 MatMul노드를 이용하여 구현하기로 했습니다
class Affine:
def __init__(self, W, b):
self.params = [W, b]
self.grads = [np.zeros_like(W), np.zeros_like(b)]
self.matmul = MatMul(W)
self.x = None
def forward(self, x):
W, b = self.params
out = self.matmul.forward(x) + b
self.x = x
return out
def backward(self, dout):
dx = self.matmul.backward(dout)
dW = self.matmul.grads[0]
db = np.sum(dout, axis=0)
self.grads[0][...] = dW
self.grads[1][...] = db
return dx
이렇게 구현한 Affine계층을 이용하여 훌륭하게 비선형 구조의 데이터를 학습한 모습입니다.

추가적으로 비트 정밀도가 낮아져도 딥러닝의 강건함(Robustness)덕분에 인식율에 큰 차이는 없지만, CPU와 GPU가 대부분 32비트 연산을 지원하기 때문에 학습 및 추론 과정에서는 float32 타입을 쓰기로 했습니다. 다만 파라미터 저장 시에는 메모리를 아끼기 위해 float16형태로 저장하기로 했습니다.
'독서' 카테고리의 다른 글
| Ch3. Word2Vec (0) | 2021.07.26 |
|---|---|
| Ch2. 자연어와 단어의 분산 표현 (0) | 2021.07.25 |
| Ch7. 합성곱 신경망 (0) | 2021.07.22 |
| Ch6. 학습 관련 기술들 (0) | 2021.07.21 |
| Ch5. 오차역전파법 (0) | 2021.07.19 |