while (1): study();

출처: https://www.acmicpc.net/problem/3665 3665번: 최종 순위 올해 ACM-ICPC 대전 인터넷 예선에는 총 n개의 팀이 참가했다. 팀은 1번부터 n번까지 번호가 매겨져 있다. 놀랍게도 올해 참가하는 팀은 작년에 참가했던 팀과 동일하다. 올해는 인터넷 예선 본부에 www.acmicpc.net 아이디어를 떠올리는 것에 상당히 애를 먹었던 문제일뿐만 아니라, 예외사항에 대해서 모두 고려해야 했던 쉽지 않았던 문제입니다. 다만 후술하겠지만 아이디어를 떠올린 이후에는 구현이 그다지 어렵지 않고, 채점 케이스도 허술하기 때문에.. 어려우면서도 쉬운(?) 문제였던 것 같습니다. 풀이 위상정렬 알고리즘을 사용하는 대표적인 문제로 '선수과목 문제'를 떠올려볼 수 있습니다. 이 문제는 ..

출처: https://www.acmicpc.net/problem/2887 2887번: 행성 터널 첫째 줄에 행성의 개수 N이 주어진다. (1 ≤ N ≤ 100,000) 다음 N개 줄에는 각 행성의 x, y, z좌표가 주어진다. 좌표는 -109보다 크거나 같고, 109보다 작거나 같은 정수이다. 한 위치에 행성이 두 개 이 www.acmicpc.net 무향그래프에 대해서 최소 신장트리를 구하는 문제이므로, 크루스칼 알고리즘을 적용하면 쉽게 풀 수 있습니다. 크루스칼 알고리즘: https://jcy1996.tistory.com/35 크루스칼 알고리즘(Kruskal Algorithm) 크루스칼 알고리즘에 대해 이해하기 위해서는 먼저 신장 트리(Spanning Tree)에 대해 이해할 필요가 있습니다. 신장 트..

문제 한 마을은 N개의 집과 M개듸 도로로 구성되어 있습니다. 각 집은 0번부터 N - 1번까지의 번호로 구분됩니다. 모든 도로에는 가로등이 구비되어 있는데, 특정한 도로의 가로등을 하루 동안 켜기 위한 비용은 해당 도로의 길이와 동일합니다. 예를 들어 2번 집과 3번 집 사이를 연결하는 길이가 7인 도로가 있다고 해봅시다. 하루 동안 이 가로등을 켜기 위한 비용은 7이 됩니다. 정부에서는 일부 가로등을 비활성화하되, 마을에 있는 임의의 두 집에 대하여 가로등이 켜진 도로만으로도 오갈 수 있도록 만들고자 합니다. 결과적으로 일부 가로등을 비활성화하여 최대한 많은 금액을 절약하고자 합니다. 마을의 집과 도로 정보가 주어졌을 때, 일부 가로등을 비활성화하여 절약할 수 있는 최대 금액을 출력하는 프로그램을 작..

문제 공항에는 G개의 탑승구가 있으며, 각각의 탑승구는 1번부터 G번까지의 번호로 구분됩니다. 공항에는 P개의 비행기가 차례대로 도착할 예정이며, i번쨰 비행기를 1번부터 $g_{i}$번째(1 $\le$ $g_{i}$ $\le$ G) 탑승구 중 하나에 영구적으로 도킹해야 합니다. 이때, 다른 비행기가 도킹하지 않은 탑승구에만 도킹할 수 있습니다. 또한 P개의 비행기를 순서대로 도킹하다가 만약에 어떠한 탑승구에도 도킹할 수 없는 비행기가 나오는 경우, 그 시점에서 공항의 운행을 중지합니다. 공항의 관리자는 최대한 많은 비행기를 공항에 도킹하고자 합니다. 비행기를 최대 몇 대 도킹할 수 있는지를 출력하는 프로그램을 작성하세요. 입력 조건 - 첫째 줄에는 탑승구의 수 G(1 $\le$ G $\le$ 100,0..

문제 한울이가 사는 나라에는 N개의 여행지가 있으며, 각 여행지는 1 ~ N번까지의 번호로 구분됩니다. 또한 임의의 두 여행지 사이에는 두 여행지를 연결하는 도로가 존재할 수 있습니다. 이때, 여행지가 도로로 연결되어 있다면 양방향으로 이동이 가능하다는 의미입니다. 한울이는 하나의 여행 계획을 세운 뒤에 이 여행 계획이 가능한지의 여부를 판단하고자 합니다. 예를 들어 N = 5이고, 다음과 같이 도로의 정보가 주어졌다고 가정합시다. 1번 여행지 - 2번 여행지 1번 여행지 - 4번 여행지 1번 여행지 - 5번 여행지 2번 여행지 - 3번 여행지 2번 여행지 - 4번 여행지 만약 한울이의 여행 계획이 2번 → 3번 → 4번 → 3번이라고 해봅시다. 이 경우 2번 → 3번 → 2번 → 4번 → 2번 → 3번..

위상 정렬 알고리즘은 방향 그래프의 모든 노드들을 방향성에 거스르지 않도록 순서대로 나열하는 정렬 기법을 의미합니다. 기존의 서로소 집합 알고리즘이나, 이를 기반으로 한 크루스칼 알고리즘은 무향 그래프에 대해서 동작했던 것을 생각하면 차이가 있습니다. 예를 들어 '선수과목을 고려한 학습 순서 설정 문제' 등에서 대표적으로 사용될 수 있습니다. 1. 각 노드의 진입차수(indegree)를 저장합니다. 2. 진입차수가 0인 노드부터 시작하여 연결된 노드에 대해 진입차수를 1씩 뺍니다. 3. 다른 노드도 진입차수가 0이 될 경우 2의 동작을 반복합니다. 큐를 사용하여 구현할 경우 위상정렬의 시간복잡도는 O(V+E)입니다. 전체 소스코드는 다음과 같습니다. input1 = '''7 8 1 2 1 5 2 3 2 ..

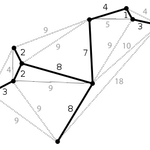
크루스칼 알고리즘에 대해 이해하기 위해서는 먼저 신장 트리(Spanning Tree)에 대해 이해할 필요가 있습니다. 신장 트리(Spanning Tree) 신장 트리는 하나의 그래프가 있을 때 모든 노드를 포함하는 부분 그래프를 의미합니다. 위의 그림이 직관적으로 신장 트리를 이해하는 데 도움이 되는 것 같습니다. 실제 그래프 관계는 훨씬 복잡하지만, 굵은 실선만 이어도 모든 노드에 대해서 연결할 수 있다는 것이 특징입니다. 크루스칼 알고리즘(Kruskal Algorithm) 크루스칼 알고리즘은 가능한 최소 비용의 신장 트리를 찾아주는 알고리즘입니다. 다음과 같은 순서로 처리됩니다. 1. 모든 간선에 대해 비용순으로 정렬을 수행합니다. 2. 거리가 짧은 간선부터 집합에 포함시킵니다. 3. 단, 사이클이 ..

서로소 집합 알고리즘 서로소 집합이란 공통 원소가 없는 두 집합을 말합니다. 따라서 어떤 그래프가 주어졌을 때 서로소 집합으로 분리하는 일련의 과정을 통해서 집합 간 관계를 파악할 수 있습니다. 이를 수행하는 알고리즘을 서로소 집합 알고리즘이라고 합니다. 서로소 집합 알고리즘은 다음과 같은 순서로 처리됩니다. 1. Union 연산을 통해 서로 연결된 두 A,B를 체크한다. 2. 모든 Union 연산을 처리할 때까지 1번 연산을 반복한다. 3. 루트를 찾기 위해서는 재귀적으로 부모를 거슬러 올라가야 한다. 위와 같이 Union연산과 확인하는 Find연산으로 구성되어 있기 때문에, Union-Find 연산이라고도 합니다. 기본적으로는 다음과 같이 코드로 구현할 수 있습니다. input1 = '''6 4 1 ..

문제 선생님은 시험을 본 학생 N명의 성적을 분실하고, 성적을 비교한 결과의 일부만 가지고 있습니다. 학생 N명의 성적은 모두 다른데, 다음은 6명의 학생에 대하여 6번만 성적을 비교한 결과입니다. - 1번 학생의 성적 < 5번 학생의 성적 - 3번 학생의 성적 < 4번 학생의 성적 - 4번 학생의 성적 < 2번 학생의 성적 - 4번 학생의 성적 < 6번 학생의 성적 - 5번 학생의 성적 < 2번 학생의 성적 - 5번 학생의 성적 < 4번 학생의 성적 순위를 정확히 알 수 있는 학생도 있고, 알 수 없는 학생도 있습니다. 학생들의 성적을 비교한 결과가 주어질 때, 성적 순위를 정확히 알 수 있는 학생은 모두 몇 명인지 계산하는 프로그램을 작성하세요. 입력 조건 - 첫째 줄에 학생들의 수 N(2

출처: https://www.acmicpc.net/problem/11404 11404번: 플로이드 첫째 줄에 도시의 개수 n이 주어지고 둘째 줄에는 버스의 개수 m이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가 www.acmicpc.net 플로이드-워셜 알고리즘을 이용한 최단경로 문제는 나오기만 하면 정말 땡큐인 문제인 듯합니다. 이 문제 역시 그래프의 노드 개수가 100개 이하이므로, 플로이드-워셜 알고리즘을 사용하여 손쉽게 해결할 수 있습니다. 플로이드-워셜 알고리즘에 대한 조금 더 상세한 설명은 다음 링크를 참조바랍니다. 링크: https://jcy1996.tistory.com/24?category=958980 플로이드..