while (1): study();

출처: https://arxiv.org/abs/1512.05287 A Theoretically Grounded Application of Dropout in Recurrent Neural Networks Recurrent neural networks (RNNs) stand at the forefront of many recent developments in deep learning. Yet a major difficulty with these models is their tendency to overfit, with dropout shown to fail when applied to recurrent layers. Recent results at the arxiv.org LSTM-LM의 성능을 개선하기 ..

드디어 최근 인공지능 SOTA의 핵심에 서있는 어텐션을 구현합니다. 이전까지 단어 간 대응 관계를 나타내는 정보인 얼라인먼트(Alignment)를 인간이 직접 만들어야만 했다면, 어텐션은 얼라인먼트조차 기계가 대신 학습한다는 점에서 큰 의미가 있습니다. 간단하게 얘기하면 인코더의 은닉상태를 입력으로 받아, 디코더의 은닉상태와 내적한 뒤 소프트맥스로 정규화하여 가중치를 구하고, 이를 이용하여 가중합을 구해 맥락 벡터(Context vector)를 생성합니다. 이전 장에서 Peeky를 이용하여 인코더의 은닉상태를 디코더의 모든 계층에 전달했었는데, Attention은 이 과정을 조금 더 효율적으로 수행하고 있습니다. 그리고 Seq2seq 모델의 관건이 인코더의 맥락을 디코더에 제대로 전달하는 것이라는 것도 ..

이번 장에서는 Vanilla RNN에서 개선된 버전인 LSTM을 구현하여 본격적인 RNN LM을 구축합니다. 기존의 Vanilla RNN은 다음과 같이 계산됩니다. $$h_{t} = tanh(h_{t-1}W_{h} + x_{t}W_{x} + b)$$ 이 때 $W_{h}$와 $W_{X}$는 계층 내에서 같은 가중치이므로, 타임스탭이 길어질 때마다 매번 같은(정확히는 비슷한) 행렬이 입력에 곱해지게 됩니다. 행렬의 최대 특잇값이 1보다 크다면 출력은 지수적으로 증가하고, 1보다 작으면 지수적으로 감소합니다. 따라서 역전파 과정에서 커지거나 작아진 가중치가 곱해지면 기울기도 그에 따라서 폭발하거나 소실될 가능성이 증가합니다. 또한 하이퍼볼릭 탄젠트 함수의 도함수가 0부터 1사이의 값을 가질 수 있기 때문에, ..

이 장에서는 이전 장에서 구현했던 Word2Vec의 속도를 개선해봅니다. 두 가지 측면에서 개선점이 있습니다. 1. Embedding layer를 이용한 입력층 연산 감소 2. Negative sampling을 이용한 출력층 연산 감소 추가적으로 단어의 밀집 벡터를 통계 기반 방법으로 얻은 경우 Distributional representation이라고 표현하며, 추론 기반 방법으로 얻은 경우 Distributed representation이라고 표현합니다. 따라서 우리는 결론적으로 최적의 Distributed representation을 얻는 것이 목표입니다. 1. Embedding layer 이전의 CBOW는 입력 가중치가 (Vocab size, Hidden size)였습니다. 입력으로 주어지는 맥락..

지금까지 자연어 처리에 대해서 공부를 하면서 많은 임베딩 기법들을 접해보았습니다. 최신의 성능좋은 기술에 눈을 돌리다보니 아무래도 그 배경에 대해서는 상대적으로 소홀했던 것 같습니다. 컴퓨터에게 인간의 언어를 이해시키는 방법론은 3가지가 있습니다. 1. 시소러스 방법론 2. 통계 기반 방법론 3. 추론 기반 방법론 이 장에선 위의 반성과 더불어 통계적으로 단어를 분산 표현으로 바꾸는 방법에 대해서 알아봅니다. 1. 시소러스 시소러스의 사전적 정의는 다음과 같습니다. 즉 시소러스 기반 방법론이란, 인간이 구축한 유의어 사전을 기반으로 단어들 간의 연관성을 컴퓨터가 파악하게 하는 것입니다. 대표적인 시소러스로는 프린스턴 대학교에서 1983년부터 구축하기 시작한 WordNet이 있습니다. WordNet은 다음..

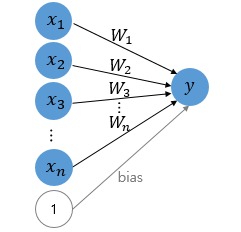
대부분의 내용이 반복인 점을 감안하여 새롭게 알게 된 내용을 위주로 작성하겠습니다. 이전 1권에서 곱셈, 덧셈 등 노드에 대해서 어떻게 역전파를 계산하는지 알아봤습니다. 기본적으로 역전파는 '상류에서 흘러들어온 기울기를 편미분'하여 하류로 흘려보냅니다. 여기서는 이전에 제시하지 않았던 종류의 노드를 제시하고 있습니다. 바로 Repeat 노드입니다. Repeat 노드의 순전파는 단순히 들어온 입력을 N번 복사하는 것입니다. 이는 np.repeat 함수로 쉽게 구현이 가능합니다. 반대로 역전파는 흘러들어오는 기울기에 대해서 모두 더해주는 과정입니다. 사실 Repeat 노드는 넘파이의 브로드캐스팅 기능으로 간단히 구현할 수 있기 때문에, 따로 모듈화할 필요는 없습니다. 이전의 기억을 잘 더듬어보면, 덧셈 노드..

출처: https://arxiv.org/abs/1502.03167 Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift Training Deep Neural Networks is complicated by the fact that the distribution of each layer's inputs changes during training, as the parameters of the previous layers change. This slows down the training by requiring lower learning rates and careful param arxiv.org 지..

이미지 처리의 기반은 CNN 아키텍처이며, CNN 아키텍처는 합성곱 연산을 사용합니다. 이는 필터와 입력 데이터에 대해서 대응하는 위치의 원소끼리 곱한 후 총합을 구하는 것입니다. 이 계산을 단일 곱셈-누산(FMA; Fused Multiply-Add)라고 합니다. 엄밀히 말하면 딥러닝에서의 연산은 교차상관이라고 부르는 것이 맞다고 합니다. 필터를 플리핑(Flipping)하면 합성곱 연산, 그렇지 않으면 교차상관입니다. 하지만 딥러닝에서 그렇게 엄밀히 구분하여 부르는 듯 하지는 않다고 하네요. 합성곱 연산을 수행하면 출력의 크기는 다음과 같이 계산됩니다. H, W는 입력의 높이와 너비, FH, FW는 필터의 높이와 너비, OH, OW는 출력의 높이와 너비, P는 패딩, S는 스트라이드를 의미합니다. $$O..

* 책 내용 요약이 아니니 유의하시기 바랍니다. 오차역전파에 대해서 이전에 해석 강의를 들은 적이 있긴 했는데, 솔직히 감이 잘 안 왔습니다. 이 책을 보고 나서야 비로소 '아! 이런거구나!'라고 제대로 와닿는 느낌이었습니다. 여러모로 읽으면 읽을수록 '읽기를 잘했다'라고 생각이 드는 책이네요. 이 책에서는 계산 그래프를 통해서 오차역전파에 대해 설명하고 있습니다. CS231n에서 설명한 방식을 차용했다고 하는데, 역시 인공지능 배우는 사람이라면 다 한번 거쳐야 하는 관문인걸까.. 싶습니다. 시간 날 때 꼭 봐야겠네요. 계산 그래프로 푸는 방법의 이점은 2가지입니다. 1. 국소적 계산: 단순한 계산에 집중하여 문제를 단순화 2. 중간 계산 결과 보관 3. 미분을 효율적으로 계산 기존 수치 미분 방법을 이..

* 책 내용 요약이 아니니 유의하시기 바랍니다. 신경망 학습 시에 '경사하강법'이라는 용어가 참 많이 나옵니다. 경사하강법이란 '손실함수가 각 가중치에 대해서 양의 기울기를 가지면 음의 방향으로, 음의 기울기를 가지면 양의 방향으로 업데이트시켜 결과적으로는 전역 최소해에 도달하게 만드는 방법'입니다. 일반적으로 다음과 같이 특정 지점의 기울기를 근사할 수 있습니다. 실제 기울기를 해석적으로 구하는 것은 컴퓨터에게 힘든 일이기 때문에, 우리는 수치 미분를 사용할 것입니다. 그중 아래와 같은 방식을 전방 차분이라고 합니다. 다만 전방 차분은 실제 해석적 기울기와는 차이가 좀 있는 편입니다. 따라서 신경망을 학습할 때는 오차를 줄이기 위해 중앙 차분을 사용합니다. 이렇게 구한 기울기는 각 장소에서 함수의 출력..